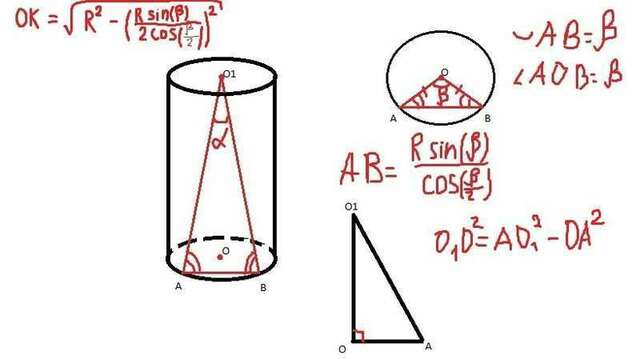
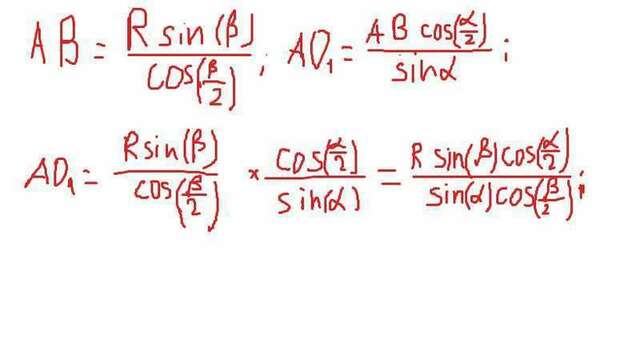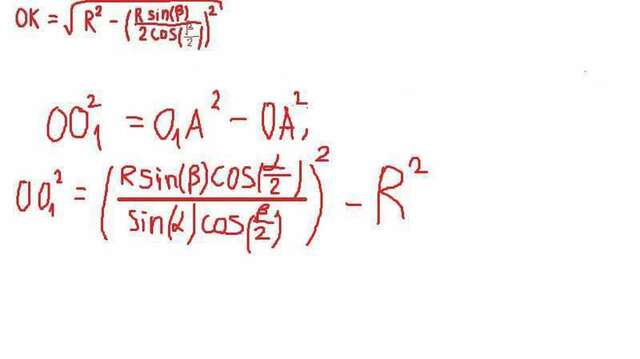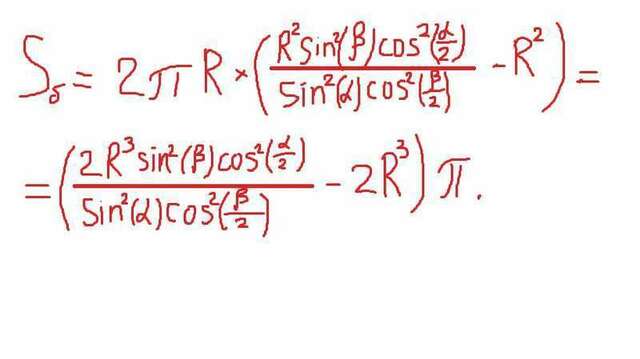Площадь боковой поверхности цилиндра равна периметру основания, умноженного на высоту, то есть S = 2*pi*R*H. R = AO = OB, H = OO1. S = 2*pi*R*OO1. Рассмотрим нижнее основание - окружность с центром О: дуга АВ равна бета, центральный угол равен радианной или градусной мере дуги, на которую опирается, а поскольку дуга АВ = бета, следовательно, центральный угол АОВ = бета. С этих пор обозначим угол альфа - α, бета - β. Из равнобедренного треугольника АОВ (поскольку АО = ВО - радиусы) Рассмотрим прямоугольный треугольник OO1A: OO1 = O1A^2 - OA^2. Пожалуй, я это лучше распишу на картинке. И площадь боковой поверхности, пожалуй, тоже.